Graph Theory and Graphs
Graphs are a mathematical tool used to model the relationship between objects. They are similar to semantic networks yet more abstract or general in scope. In computer science, graphs are a new and powerful data structure whose implementation in C++ we shall discuss further down. Still you could buy or download a graph database, which is a graph plus some means of serialization, commandline querying etc.
Graphs are made up of nodes (vertices) and arcs (edges). Each edge connects two nodes, unless it is a self-edge, which connects a vertex or node to itself.
Nodes represent entities and hold some content, whereas arcs represent relationships. In a weighted graph arcs hold a value or some other information, called its weight because it is often meant to represent the cost
of going from the start of the arc to the end of the arc.
The next figure depicts a directed graph with five vertices (labeled 0 through 4) and 11 edges. The edges leaving a vertex are called the out-edges of the vertex. The edges {(0,1),(0,2),(0,3),(0,4)} are all out-edges of vertex 0. The edges entering a vertex are called the in-edges of the vertex. The edges {(0,4),(2,4),(3,4)} are all in-edges of vertex 4.
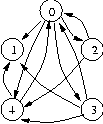
A path through a graph connects a sequence of nodes through successive arcs. The path is represented by an ordered list that records the nodes in the order they occur in the path. A path that leads back to its first node is said to be a cycle or loop and a path that at some point crosses itself is said to contain a cycle or loop.
A rooted graph has a unique node, called the root, such that there is a path from the root to all nodes within the graph. In drawing a rooted graph, the root is usually placed at the top of the page, above the other nodes. The state space graphs for games are usually rooted graphs with the start of the game as the root.
A tree is a graph in which two nodes have at most one path between them. Trees often have roots, in which case they are usually drawn with the root at the top, like a rooted graph. Because each node in a tree has only one path of access from any other node, it is impossible for a path to loop or cycle through a sequence of nodes.
For rooted trees or graphs, relationships between nodes include parent, child, and sibling. These are used in the usual familial fashion with the parent preceding its child along a directed arc. The children of a node are called siblings. Similarly, an ancestor comes before a descendant in some path of a directed graph.
A tip or leaf node is a node that has no children.
Graph Examples, Problems, and Applications
Some situations that are suitably modeled through a graph or some instances of graphs are:
- a road map showing towns (objects) and the roads that link them up (relationships), where each road may bear a length weight, or
- the schematic of an electronic circuit, where electronic components are objects and connecting wires are relationships between them (possibly bearing weights such as delay and complex impedance), or
- a Finate State Machine, whose states are graph nodes and whose transitions are weighted arcs, or
- a diagram of events that cause or preclude other events
- nearly anything else that is understood in terms of entities and relationships.
A famous graph problem has been that of coloring a planar map so that no two adjacent regions have the same color. In 1976 it was proved that yes, just four colors are sufficient to color any planar map.
Directed Graphs
In a directed graph arcs are traversed in one direction. If there is another arc in the opposite direction and the graph is weighted, the weights may be different.
Are electronic schematics directed or indirected graphs?
Wires are no doubt undirected, but some components realize a control function so we tend to analize schematics in terms of cause and effect.
Typed Graphs*
The State Space Representation of Problems
In the state space representation of a problem, the nodes of a graph correspond to partial problem solution states and the arcs correspond to steps in a problem-solving process. One or more initial states, corresponding to the given information in a problem instance, form the root of the graph. The graph also defines one or more goal conditions, which are solutions to a problem instance. State space search characterizes problem solving as the process of finding a solution path from the start state to a goal.
A goal may describe a state, such as a winning board in tic-tac-toe or a goal configuration in the 8-puzzle. Alternatively, a goal can describe some property of the solution path itself. In the traveling salesperson problem, search terminates when the shortest
path is found through all nodes of the graph. In the parsing problem, the solution path is a successful analysis of a sentence's structure.
Arcs of the state space correspond to steps in a solution process and paths through the space represent solutions in various stages of completion. Paths are searched, beginning at the start state and continuing through the graph, until either the goal description is satisfied or they are abandoned. The actual generation of new states along the path is done by applying operators, such as legal moves
in a game or inference rules in a logic problem or expert system, to existing states on a path. The task of a search algorithm is to find a solution path through such a problem space. Search algorithms must keep track of the paths from a start to a goal node, because these paths contain the series of operations that lead to the problem solution.
We now formally define the state space representation of problems:
Definition of State Space Search
A state space is represented by a four-tuple [N,A,S,GD], where:
-
N is the set of nodes or states of the graph. These correspond to the states in a problem-solving process.
-
A is the set of arcs (or links) between nodes. These correspond to the steps in a problem-solving process.
-
S, a nonempty subset of N, contains the start state(s) of the problem.
-
GD, a nonempty subset of N, contains the goal state(s) of the problem. The states in GD are described using either:
- 1. A measurable property of the states encountered in the search.
- 2. A measurable property of the path developed in the search, for example, the sum of the transition costs for the arcs of the path.
A solution path is a path through this graph from a node in S to a node in GD.
Strategies for State Space Search
Data-Driven and Goal-Driven Search
A state space may be searched in two directions: from the given data of a problem instance toward a goal or from a goal back to the data.
In data-driven search, sometimes called forward chaining, the problem solver begins with the given facts of the problem and a set of legal moves or rules for changing state. Search proceeds by applying rules to facts to produce new facts, which are in turn used by the rules to generate more new facts. This process continues until (we hope!) it generates a path that satisfies the goal condition.
An alternative approach is possible: take the goal that we want to solve. See what rules or legal moves could be used to generate this goal and determine what conditions must be true to use them. These conditions become the new goals, or subgoals, for the search. Search continues, working backward through successive subgoals until (we hope!) it works back to the facts of the problem. This finds the chain of moves or rules leading from data to a goal, although it does so in backward order. This approach is called goal-driven reasoning, or backward chaining, and it recalls the simple childhood trick of trying to solve a maze by working back from the finish to the start.
To summarize: data-driven reasoning takes the facts of the problem and applies the rules or legal moves to produce new facts that lead to a goal; goal-driven reasoning focuses on the goal, finds the rules that could produce the goal, and chains backward through successive rules and subgoals to the given facts of the problem.
In the final analysis, both data-driven and goal-driven problem solvers search the same state space graph; however, the order and actual number of states searched can differ. The preferred strategy is determined by the properties of the problem itself. These include the complexity of the rules, the shape
of the state space, and the nature and availability of the problem data. All of these vary for different problems.
An Example of Data- and Goal-Driven Search
As an example of the effect a search strategy can have on the complexity of search, consider the problem of confirming or denying the statement I am a descendant of Thomas Jefferson.
A solution is a path of direct lineage between the I
and Thomas Jefferson. This space may be searched in two directions, starting with the I
and working along ancestor lines to Thomas Jefferson or starting with Thomas Jefferson and working through his descendants.
Some simple assumptions let us estimate the size of the space searched in each direction. Thomas Jefferson was born about 250 years ago; if we assume 25 years per generation, the required path will be about length 10. As each person has exactly two parents, a search back from the I
would examine on the order of 210 ancestors. A search that worked forward from Thomas Jefferson would examine more states, as people tend to have more than two children (particularly in the eighteenth and nineteenth centuries). If we assume an average of only three children per family, the search would examine on the order of 310 nodes of the family tree. Thus, a search back from the I
would examine fewer nodes. Note, however, that both directions yield exponential complexity.
Choosing between Data- And Goal-Driven Search
The decision to choose between data- and goal-driven search is based on the structure of the problem to be solved. Goal-driven search is suggested if:
- 1. A goal or hypothesis is given in the problem statement or can easily be formulated. In a mathematics theorem prover, for example, the goal is the theorem to be proved. Many diagnostic systems consider potential diagnoses in a systematic fashion, confirming or eliminating them using goal-driven reasoning.
- 2. There are a large number of rules that match the facts of the problem and thus produce an increasing number of conclusions or goals. Early selection of a goal can eliminate most of these branches, making goal-driven search more effective in pruning the space. In a theorem prover, for example, the total number of rules used to produce a given theorem is usually much smaller than the number of rules that may be applied to the entire set of axioms.
- 3. Problem data are not given but must be acquired by the problem solver. In this case, goal-driven search can help guide data acquisition. In a medical diagnosis program, for example, a wide range of diagnostic tests can be applied. Doctors order only those that are necessary to confirm or deny a particular hypothesis.
Goal-driven search thus uses knowledge of the desired goal to guide the search through relevant rules and eliminate branches of the space.
Data-driven search is appropriate for problems in which:
- 1. All or most of the data are given in the initial problem statement. Interpretation problems often fit this mold by presenting a collection of data and asking the system to provide a high-level interpretation. Systems that analyze particular data (e.g., the PROSPECTOR or Dipmeter programs, which interpret geological data or attempt to find what minerals are likely to be found at a site) fit the data-driven approach.
- 2. There are a large number of potential goals, but there are only a few ways to use the facts and given information of a particular problem instance. The DENDRAL program, an expert system that finds the molecular structure of organic compounds based on their formula, mass spectrographic data, and knowledge of chemistry, is an example of this. For any organic compound, there are an enormous number of possible structures. However, the mass spectrographic data on a compound allow DENDRAL to eliminate all but a few of these.
- 3. It is difficult to form a goal or hypothesis. In using DENDRAL, for example, little may be known initially about the possible structure of a compound.
Data-driven search uses the knowledge and constraints found in the given data of a problem to guide search along lines known to be true.
To summarize, there is no substitute for careful analysis of the particular problem to be solved, considering such issues as the branching factor of rule applications (on average, how many new states are generated by rule applications in both directions?), availability of data, and ease of determining potential goals.
Implementing Graph Search
In solving a problem using either goal- or data-driven search, a problem solver must find a path from a start state to a goal through the state space graph. The sequence of arcs in this path corresponds to the ordered steps of the solution. If a problem solver were given an oracle or other infallible mechanism for choosing a solution path, search would not be required. The problem solver would move unerringly through the space to the desired goal, constructing the path as it went. Because oracles do not exist for interesting problems, a problem solver must consider different paths through the space until it finds a goal. Backtracking is a technique for systematically trying all paths through a state space. We begin with backtrack because it is one of the first search algorithms computer scientists study, and it has a natural implementation in a stack oriented recursive environment. We will present a simpler version of the backtrack algorithm with depth-first search.
Backtracking search begins at the start state and pursues a path until it reaches either a goal or a dead end.
If it finds a goal, it quits and returns the solution path. If it reaches a dead end, it backtracks
to the most recent node on the path having unexamined siblings and continues down one of these branches, as described in the following recursive rule:
If the present state S does not meet the requirements of the goal description, then generate its first descendant Schild1, and apply the backtrack procedure recursively to this node. If backtrack does not find a goal node in the subgraph rooted at Schild1, repeat the procedure for its sibling, Schild2. Continue until either some descendant of a child is a goal node or all the children have been searched. If none of the children of S leads to a goal, then backtrackfails backto the parent of S, where it is applied to the siblings of S, and so on.
The algorithm continues until it finds a goal or exhausts the state space. We now define an algorithm that performs a backtrack, using three lists to keep track of nodes in the state space:
- SL, for state list, lists the states in the current path being tried. If a goal is found, SL contains the ordered list of states on the solution path.
- NSL, for new state list, contains nodes awaiting evaluation, i.e., nodes whose descendants have not yet been generated and searched.
- DE, for dead ends, lists states whose descendants have failed to contain a goal. If these states are encountered again, they will be detected as elements of DE and eliminated from consideration immediately.
In defining the backtrack algorithm for the general case (a graph rather than a tree), it is necessary to detect multiple occurrences of any state so that it will not be reentered and cause (infinite) loops in the path. This is accomplished by testing each newly generated state for membership in any of these three lists. If a new state belongs to any of these lists, then it has already been visited and may be ignored.
This is the pseudocode for function
function backtrack;
begin
SL := [Start]; NSL := [Start]; DE := [ ]; CS := Start; % initialize:
while NSL ≠ [ ] do % while there are states to be tried
begin
if CS = goal (or meets goal description)
then return SL; % on success, return list of states in path.
if CS has no children (excluding nodes already on DE, SL, and NSL)
then begin
while SL is not empty and CS = the first element of SL do
begin
add CS to DE; % record state as dead end
remove first element from SL; %backtrack
remove first element from NSL;
CS := first element of NSL;
end
add CS to SL;
end
else begin
place children of CS (except nodes already on DE, SL, or NSL) on NSL;
CS := first element of NSL;
add CS to SL
end
end;
return FAIL;
end.
In frontier
of the solution path currently being explored. Inference rules, moves in a game, or other appropriate problem-solving operators are ordered and applied to CS. The result is an ordered set of new states, the children of CS. The first of these children is made the new current state and the rest are placed in order on NSL for future examination. The new current state is added to SL and search continues. If CS has no children, it is removed from SL (this is where the algorithm backtracks
) and any remaining children of its predecessor on SL are examined.
As presented here,
- 1. The use of a list of unprocessed states (NSL) to allow the algorithm to return to any of these states.
- 2. A list of
bad
states (DE) to prevent the algorithm from retrying useless paths. - 3. A list of nodes (SL) on the current solution path that is returned if a goal is found.
- 4. Explicit checks for membership of new states in these lists to prevent looping.
Data Structures for Graphs
Vertices or nodes are often represented by some identifiers. The shortest identifier is an (positive or unsigned) integer.
Edges are often represented by ordered pairs.
- Adjacency Lists
- Adjacency Matrix
-
These are good for representing very dense, that is interconnected, graphs, where each vertex is connected to nearly every other vertex.
- Edge Lists
-
An edge list is just a list of edges.
Internal and External Properties
The properties of vertices and edges can be stored inside the the graph data structure or outside in some suitably addressable data structure, such as an array or an associative map.
Graph Algorithms
Algorithms for Finding the Shortest Path
We want to find the shortest path from one vertex to all other vertices. We start with a weighted (undirected) graph
This graph could be represented using an adjacency list adj[][] (C/C++ syntax), where each entry adj[u] contains pairs of the form {v, w} - representing that vertex u is connected to vertex v with an edge weight of w and we are also given a source vertex src. We need to find the shortest path distances from the source vertex to all other vertices in the graph.
Note The given graph does not contain any negative edge.
Example:
Input: src = 0, adj[][] = [[[1, 4], [2, 8]],
[[0, 4], [4, 6], [2,3]],
[[0, 8], [3, 2], [1,3]],
[[2, 2], [4, 10]],
[[1, 6], [3, 10]]]
Dijkstra's Shortest Path Algorithm
(Heavily from https://www.w3schools.com/dsa/dsa_algo_graphs_dijkstra.php)
Dijkstra's algorithm finds the shortest path from one vertex to all other vertices by repeatedly selecting the nearest unvisited vertex and calculating the distance to all the unvisited neighboring vertices.
Often considered to be the most straightforward algorithm for solving the shortest path problem.
Dijkstra's algorithm is used for solving single-source shortest path problems for directed or undirected paths. Single-source means that one vertex is chosen to be the start, and the algorithm will find the shortest path from that vertex to all other vertices.
Dijkstra's algorithm does not work for graphs with negative edges. For graphs with negative edges, the Bellman-Ford algorithm, can be used instead.
To find the shortest path, Dijkstra's algorithm needs to know which vertex is the source, it needs a way to mark vertices as visited, and it needs a record of the current shortest distance to each vertex as it works its way through the graph, updating these distances when a shorter distance is found.
Steps:
- Set initial distances for all vertices: 0 for the source vertex, and infinity for all the other.
- Choose the unvisited vertex with the shortest distance from the start to be the current vertex. So the algorithm will always start with the source as the current vertex.
- For each of the current vertex's unvisited neighbor vertices, calculate the distance from the source and update the distance if the new, calculated, distance is lower.
- We are now done with the current vertex, so we mark it as visited. A visited vertex is not checked again.
- Go back to step 2 to choose a new current vertex, and keep repeating these steps until all vertices are visited.
- In the end we are left with the shortest path from the source vertex to every other vertex in the graph.
Note: This basic version of Dijkstra's algorithm gives us the value of the shortest path cost to every vertex, but not what the actual path is.
Bellman-Ford Algorithm*
Topological Sort
One of the most useful algorithms on graphs is topological sort, in which the nodes of an acyclic graph are placed in a total order consistent with the edges of the graph; that is, if there is an edge (u,v), then u comes before v in the resulting total order. This is useful when you need to order a set of elements and some elements have no ordering constraint relative to other elements.
For example, suppose you have a set of tasks to perform, but some tasks have to be done before other tasks can start. In what order should you perform the tasks? This problem can be solved by representing the tasks as nodes in a graph with an edge from task1 to task2 if task1 must be done before task2. A topological sort of the graph will give an ordering in which all of these constraints are satisfied.
Of course, it is impossible to topologically sort a graph with a cycle in it. So to topologically sort a graph, it must be a DAG. But the interesting thing is that the condition of being a DAG is not only necessary for the existence of a topological sort, it is also sufficient. That is, all DAGs have at least one topological sort.
We can obtain a linear-time algorithm for topological sort from DFS. The key observation is that a node finishes (is marked black) only after all of its descendants have been marked black. Therefore, a node that is marked black later must come earlier when topologically sorted. A a postorder traversal generates nodes in the reverse of a topological sort:
[...]
Minimum Spanning Tree*
(From https://www.w3schools.com/dsa/dsa_theory_mst_minspantree.php)
Sparse Matrices*
How to Implement a Graph Data Structure
A graph can be implemented as a container of containers or as a (possibly sparse) matrix.
- A graph as a container of containers
-
When a graph is implemented as a container of containers, the elements of the outer container are each a pair holding:
-
The contents of or a reference to a node where arcs or edges originate
-
Another,
inner
container holding as elements the contents of or a reference to each of the nodes at the other end of the arc or edge that each of these elements represents. In the case of weighted graphs, the elements of the inner container are
You can choose almost any container or data structure capable of holding elements as long as it is enumerable. If you know how many nodes the graph shall have as well as their contents beforehand, you may choose a fixed-sized array such as a C-array in C or a more
intelligent
array such as an std::array or an std::vector if you want it to grow in size. -
- A graph as a (sparse) matrix
-
When a graph is implemented as a 2-dimensional matrix or as a sparse matrix, the matrix must be square (there must be as many rows as there are columns) and there must be as many rows or columns as there are nodes in the graph.
Element ei,j represents an arc or edge from the ith node to the jth node. The contents of ei,j must denote whether there is an arc or edge or not from the ith to the jth node. Additionally, if the graph is weighted, then the contents is the weight of the existing arc or edge, typically a number.
This is a matrix representation of the graph of the distances (km) between three Spanish cities: Barcelona, Bilbao and Madrid:
/ 0 632 654 \ | 632 0 432 | \ 654 432 0 /
If there were no road between two given cities, we would need some device such as using a negative number, or a weight of zero, or an ordered pair of a true-false value plus a weight.
If there may be several routes and thus several different distances between two cities, then each element in the matrix must be able to hold a set of distances...
Once we have a graph data structure in place, we need a means to search it.
Ordered Sets of Arcs/Edges
In choosing the data structures suitable for implementing a graph, we must decide whether we want the arcs or edges to be ordered, that is whether it makes sense to maintain that a given edge is the jth edge of all that leave the ith node, or at least whether for each arc an its successor an+1 can be found, as long as an is not the last
arc leaving a node.
Depth-first search algorithms in particular require that arcs be next-able when they backtrack to a previous, unexhausted node to resume digging.
Hypergraphs
In mathematics, a hypergraph is a generalization of a graph in which an edge can connect any number of vertices. Formally, a hypergraph H is a pair
WikipediaH = (X,E) where X is a set of elements called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or edges. Therefore, E is a subset of P(X)\{0}, the power set of X less the empty set.

In a hypergraph, edges link elements to sets of elements.
Another way to view hypergraphs is to consider that while the edges of a (directed) graph have (ordered) pairs of [references to] nodes, the edges of a hypergraph, or hyperedges, are either an ordered pair of a source node and a set of destination nodes, or just tuples where, say, the first element is [a reference to] the source node and the remainder are [references to] destination nodes.
It is often desirable to study hypergraphs where all hyperedges have the same cardinality; a k-uniform hypergraph is a hypergraph such that all its hyperedges have size k. (In other words, one such hypergraph is a collection of sets, each such set a hyperedge connecting k nodes.) So a 2-uniform hypergraph is a graph, a 3-uniform hypergraph is a collection of unordered triples, and so on.
Ordered, Directed or Tuple Hypergraphs
In a tuple hypergraph the edges are not sets (unordered) but tuples (ordered). This enables modelling the sentences in a natural language, thus extending the expressive power of semantic networks.
Semantic networks are good for representing binary relationships between objects. In Andrew knows Philip
, Andrew and Philip represent entities, and know might be represented as a weight in a graph. We would also succeed in representing sentences like Anne knows Italy
, or Anne lives in Italy
, if it is understood that the weight of the latter is live(s) in
. But the model cannot represent sentences like Mary writes novels on a computer
because here write(s) is being used as a ternary relationship. This relationship could be expressed through an edge consisting of an entity and a tuple of two entities (a pair), or through a tuple of three entities. And so on.
Variations
- A hypergraph may be a std::multimap<Node&, std::set<Node&> >,
- hyperarcs might be arrays of nodes: typedef std::vector<Node&> hyperarc;
Formal Mapping Between Graphs and Hypergraphs
Both graphs and hypergraphs have nodes. They differ in whether they connect their nodes through edges or through hyperedges. The way to map between a graph and a hypergraph relies on the concept of typed graphs:
- a graph node's children are hyperedge nodes, that is nodes whose children are non-hyperedge nodes...
- ...
A weighted graph can model the hyperedges in a phypergraph like this:
- Either a graph have two types of nodes, one representing objects or nodes in a hypergraph and the other representing relationships between object nodes,
- or ...
Predicators
Imagine a universe of entities (objects, persons, words etc.). Programmatically, these might be held in an array (std::vector), a linked list, an std::set etc.
On top of this we might want to build a layer of first-order predicators, that is predicates that take 0 to n references to entities in the bottom layer, as in cry(John). Programmatically, predicators would have a container objects such as an array or even a linked list (since growing a list never invalidates pointers to its members).
Next, a layer of second order predicators would hold predicates on first order predicators, for example cause(cry(John), wakeup(Peter)).
And so on. Note that predicates of different order would all have a container for their predicates, whereas atomic entities would not. But what about predicates that take arguments of mixed-order, as in know(I, sleep(Peter))? May be we would want to derive both predicates and entities from an ancestor Entity class and resolve types polymorphically should the need arise.
Hypergraphs and the Entity-Relationship Model
Ordered or tuple hypergraphs can be used to represent simple and compound sentences in a language. The texts or sentences of a language are made up of entities (noun phrases) and relationships or predications on entities and relationships themselves.
A linguistical hypergraph would have two kinds of nodes: entity nodes and relationship nodes...
Maximum Flow
(Heavily and gratefully from https://www.w3schools.com/dsa/dsa_theory_graphs_maxflow.php)
The Maximum Flow problem is about finding the maximum flow through a directed graph, from one place in the graph to another.
More specifically, the flow comes from a source vertex s, and ends up in a sink vertex t, and each edge in the graph is defined with a flow and a capacity, where the capacity is the maximum flow that edge can have.
Finding the maximum flow can be very useful:
- For planning roads in a city to avoid future traffic jams.
- To assess the effect of removing a water pipe, or electrical wire, or network cable.
- To find out where in the flow network expanding the capacity will lead to the highest maximum flow, with the purpose of increasing for example traffic, data traffic, or water flow.
Terminology And Concepts
A flow network if often what we call a directed graph with a flow flowing through it.
The capacity c of an edge tells us how much flow is allowed to flow through that edge. Each edge also has a flow value that tells how much the current flow is in that edge. For instance 3/7 might represent a flow of 3 and a capacity of 7. The flow cannot be greater than the capacity.
In its simplest form, a flow network has one source vertex s where the flow comes out, and one sink vertex t where the flow goes in. The other vertices just have flow passing through them.
For all vertices except s and t, there is a conservation of flow, which means that the same amount of flow that goes into a vertex, must also come out of it.
The maximum flow is found by algorithms such as Ford-Fulkerson, or Edmonds-Karp, by sending more and more flow through the edges in the flow network until the capacity of the edges are such that no more flow can be sent through. Such a path where more flow can be sent through is called an augmented path.
Residual Network
The Ford-Fulkerson and Edmonds-Karp algorithms are implemented using something called a residual network. This will be explained in more detail on the next pages.
The residual network is set up with the residual capacities on each edge, where the residual capacity of an edge is the capacity on that edge, minus the flow. So when flow is increased in an edge, the residual capacity is decreased with the same amount.
For each edge in the residual network, there is also a reversed edge that points in the opposite direction of the original edge. The residual capacity of a reversed edge is the flow of the original edge. Reversed edges are important for sending flow back on an edge as part of the maximum flow algorithms.
Multiple Source and Sink Vertices
The Ford-Fulkerson and Edmonds-Karp algorithms expects one source vertex and one sink vertex to be able to find the maximum flow.
If the graph has more than one source vertex, or more than one sink vertex, the graph should be modified to find the maximum flow.
To modify the graph so that you can run the Ford-Fulkerson or Edmonds-Karp algorithm on it, create an extra super-source vertex if you have multiple source vertices, and create an extra super-sink vertex if you have multiple sink-vertices.
From the super-source vertex, create edges to the original source vertices, with infinite capacities. And create edges from the sink vertices to the super-sink vertex similarly, with infinite capacities.
The Ford-Fulkerson or Edmonds-Karp algorithm is now able to find maximum flow in a graph with multiple source and sink vertices, by going from the super source S, to the super sink T.
The Max-flow Min-cut Theorem
To understand what this theorem says we first need to know what a cut is.
We create two sets of vertices: one with only the source vertex inside it called S, and one with all the other vertices inside it (including the sink vertex) called T. Now, starting in the source vertex, we can choose to expand set S by including adjacent vertices and excluding them from T, and continue to include adjacent vertices as much as we want as long as we do not include the sink vertex.
Expanding set S will shrink set T, because any vertex belongs either to set S or set T.
In such a setup, with any vertex belonging to either set S or set T, there is a cut between the sets. The cut consists of all the edges stretching from set S to set T.
If we add all the capacities from edges going from set S to set T, we get the capacity of the cut, which is the total possible flow from source to sink in this cut.
The minimum cut is the cut we can make with the lowest total capacity, which will be the bottleneck.
The max-flow min-cut theorem says that finding the minimum cut in a graph, is the same as finding the maximum flow, because the value of the minimum cut will be the same value as the maximum flow.
Practical Implications of The Max-flow Min-cut Theorem
Finding the maximum flow in a graph using an algorithm like Ford-Fulkerson also helps us to understand where the minimum cut is: The minimum cut will be where the edges have reached full capacity. It will be where the bottleneck is, so if we want to increase flow beyond the maximum limit, which is often the case in practical situations, we now know which edges in the graph that needs to be modified to increase the overall flow.
Modifying edges in the minimum cut to allow more flow can be very useful in many situations:
- Better traffic flow can be achieved because city planners now know where to create extra lanes, where to re-route traffic, or where to optimize traffic signals.
- In manufacturing, a higher production output can be reached by targeting improvements where the bottleneck is, by upgrading equipment or reallocating resources for example.
- In logistics, knowing where the bottleneck is, the supply chain can be optimized by changing routes, or increase capacity at critical points, ensuring that goods are moved more effectively from warehouses to consumers.
So using maximum flow algorithms to find the minimum cut, helps us to understand where the system can be modified to allow an even higher throughput.
The Maximum Flow Problem Described Mathematically
The maximum flow problem is not just a topic in Computer Science, it is also a type of Mathematical Optimization, that belongs to the field of Mathematics.
In case you want to understand this better mathematically, the maximum flow problem is described in mathematical terms below.
All edges (E ) in the graph, going from a vertex (u) to a vertex (v), have a flow (f) that is less than, or equal to, the capacity (c ) of that edge:
∀(u,v) ∈ E: f(u,v) ≤ c(u,v)
This basically just means that the flow in an edge is limited by the capacity in that edge.
Also, for all edges (E ), a flow in one direction from u to v is the same as having a negative flow in the reverse direction, from v to u:
∀(u,v) ∈ E : f(u,v) = −f(v,u)
And the expression below states that conservation of flow is kept for all vertices (u ) except for the source vertex (s) and for the sink vertex (t ):
∀u ∈ V {s,t} ⇒ ∑w∈V f(u,w) = 0
This just means that the amount of flow going into a vertex, is the same amount of flow that comes out of that vertex (except for the source and sink vertices).
And at last, all flow leaving the source vertex s , must end up in the sink vertex t:
∑(s,u) ∈ E f(s,u) = ∑(v,t)∈E f(v,t)
The equation above states that adding all flow going out on edges from the source vertex will give us the same sum as adding the flow in all edges going into the sink vertex.
Ford-Fulkerson Algorithm
(From https://www.w3schools.com/dsa/dsa_algo_graphs_fordfulkerson.php)
The Ford-Fulkerson algorithm works by looking for a path with available capacity from the source to the sink (called an augmented path), and then sends as much flow as possible through that path. The Ford-Fulkerson algorithm continues to find new paths to send more flow through until the maximum flow is reached.
Note: The Ford-Fulkerson algorithm is often described as a method instead of as an algorithm, because it does not specify how to find a path where flow can be increased. This means it can be implemented in different ways, resulting in different time complexities. But we will call it an algorithm here, and use Depth-First-Search to find the paths.
Residual Network in Ford-Fulkerson
The Ford-Fulkerson algorithm actually works by creating and using something called a residual network, which is a representation of the original graph. In the residual network, every edge has a residual capacity, which is the original capacity of the edge, minus the the flow in that edge. The residual capacity can be seen as the leftover capacity in an edge with some flow.
For example, if there is a flow of 2 in the v3→v4 edge, and the capacity is 3, the residual flow is 1 in that edge, because there is room for sending 1 more unit of flow through that edge.
Reversed Edges in Ford-Fulkerson
The Ford-Fulkerson algorithm also uses something called reversed edges to send flow back. This is useful to increase the total flow.
To send flow back, in the opposite direction of the edge, a reverse edge is created for each original edge in the network. The Ford-Fulkerson algorithm can then use these reverse edges to send flow in the reverse direction.
A reversed edge has no flow or capacity, just residual capacity. The residual capacity for a reversed edge is always the same as the flow in the corresponding original edge.
The idea of a residual network with residual capacity on edges, and the idea of reversed edges, are central to how the Ford-Fulkerson algorithm works.
Edmonds-Karp Algorithm
(From https://www.w3schools.com/dsa/dsa_algo_graphs_edmondskarp.php)
The Edmonds-Karp algorithm is very similar to the Ford-Fulkerson algorithm, except the Edmonds-Karp algorithm uses Breadth First Search (BFS) to find augmented paths to increase flow.
The Edmonds-Karp algorithm works by using Breadth-First Search (BFS) to find a path with available capacity from the source to the sink (called an augmented path), and then sends as much flow as possible through that path. It continues to find new paths to send more flow through until the maximum flow is reached.